cinématique.

cinématique. n.f., étude du mouvement d'un corps indépendamment des causes qui produisent ce mouvement. La notion du mouvement est relative : une personne marchant sur un tapis roulant a un certain mouvement par rapport au tapis et un autre mouvement par rapport à la Terre. Il faudra toujours commencer par choisir un repère, c'est-à-dire un système d'axes Oxyz. Ce repère peut être un repère lié à la surface de la Terre ; il servira à étudier les mouvements sur la Terre (par exemple ceux des automobiles). Il peut aussi avoir son origine au centre de la Terre et être lié aux étoiles fixes ; il servira à étudier le mouvement des satellites. Le repère peut aussi avoir pour origine le centre du Soleil pour étudier le mouvement des planètes. Il faut aussi repérer le temps. Pour étudier le mouvement d'un solide, on étudie d'abord le mouvement de son centre d'inertie, qui est le point du solide dont le mouvement est le plus simple. On étudie après cela le mouvement du corps par rapport à son centre d'inertie (rotation, déformation). Ici, nous ne considérerons que le mouvement du point. Vecteur position. À un instant donné, la position du point M est définie par le vecteur position , O étant l'origine. Vecteur vitesse. Au cours du temps, le point M se déplace sur sa trajectoire, il a une vitesse. Le vecteur vitesse ¯ indique comment varie le vecteur position au cours du temps : c'est la dérivée par rapport au temps t du vecteur position ¯ = d()/dt. Le vecteur vitesse est tangent à la trajectoire, il est orienté dans le sens du mouvement. Vecteur accélération. Si, au cours du temps, la vitesse varie, le point a une accélération. Le vecteur accélération D indique comment varie le vecteur vitesse au cours du temps : c'est la dérivée par rapport au temps du vecteur vitesse : D = d¯/dt. Le vecteur accélération est toujours dirigé vers l'intérieur de la trajectoire si elle est courbe. La connaissance du mouvement du point permet donc de connaître son accélération. Inversement, connaissant l'accélération d'un point et ses position et vitesse initiales, on peut déterminer son mouvement. Par ailleurs la mécanique newtonienne exprime la proportionnalité entre les forces et les accélérations. On voit ainsi que les forces sont les causes physiques du mouvement et l'on comprend l'intérêt de la cinématique pour la mécanique. Mouvement rectiligne. Si la trajectoire est une droite, le mouvement est rectiligne. Si la vitesse est constante, le mouvement est dit rectiligne uniforme ; l'accélération est alors nulle. C'est le mouvement le plus simple qui soit, par exemple celui d'une automobile roulant à vitesse constante sur une route droite. 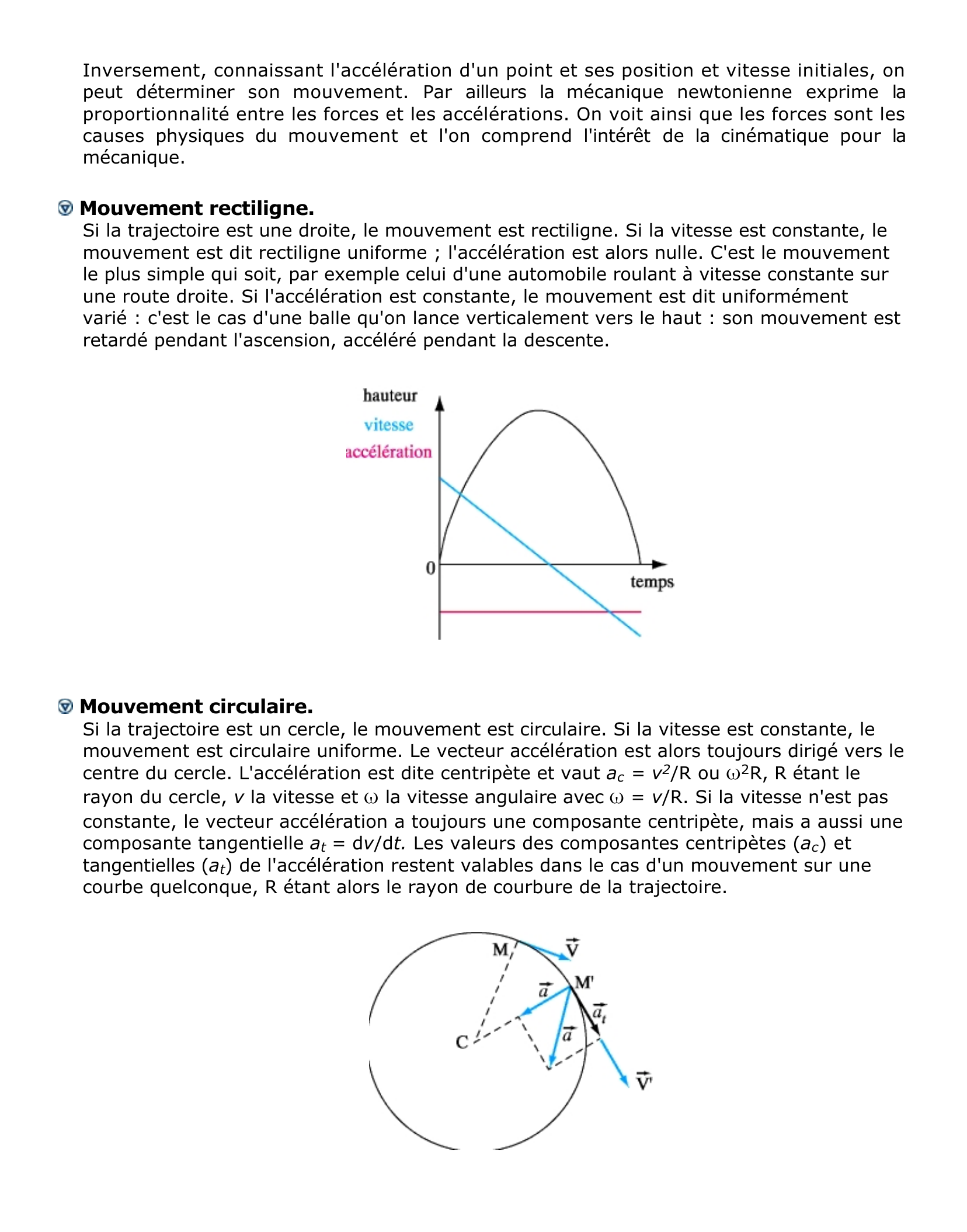Si l'accélération est constante, le mouvement est dit uniformément varié : c'est le cas d'une balle qu'on lance verticalement vers le haut : son mouvement est retardé pendant l'ascension, accéléré pendant la descente. Mouvement circulaire. Si la trajectoire est un cercle, le mouvement est circulaire. Si la vitesse est constante, le mouvement est circulaire uniforme. Le vecteur accélération est alors toujours dirigé vers le centre du cercle. L'accélération est dite centripète et vaut ac = v2/R ou w2R, R étant le rayon du cercle, v la vitesse et w la vitesse angulaire avec w = v/R. Si la vitesse n'est pas constante, le vecteur accélération a toujours une composante centripète, mais a aussi une composante tangentielle at = dv/dt. Les valeurs des composantes centripètes (ac) et tangentielles (at) de l'accélération restent valables dans le cas d'un mouvement sur une courbe quelconque, R étant alors le rayon de courbure de la trajectoire. Mouvement relatif. Le mouvement relatif est le mouvement par rapport à un repère lui-même en mouvement. Si le point a par rapport au repère en mouvement une vitesse relative ¯r et si le repère en mouvement a par rapport à un repère fixe une vitesse d'entraînement ¯e , le point a par rapport au repère fixe une vitesse absolue ¯a = ¯e + ¯r . Pour les accélérations, il apparaît une accélération complémentaire dite de Coriolis qui se manifeste si le repère en mouvement a un mouvement de rotation par rapport au repère fixe et si le corps n'est pas au repos par rapport au repère en mouvement. Cette accélération permet d'expliquer que le vent, au lieu de se diriger directement des hautes vers les basses pressions, s'enroule en spirale dans le sens contraire des aiguilles d'une montre dans l'hémisphère nord et en sens inverse dans l'hémisphère sud. Complétez votre recherche en consultant : Les corrélats accélération centrifuge (force) centripète (force) choc - 1.PHYSIQUE Coriolis Gustave Gaspard mécanique - 1.PHYSIQUE mouvement [1] - 2.MATHÉMATIQUES Newton (Isaac) physique - La révolution galiléenne et la naissance de la physique classique - De Galilée à Newton repère sciences (histoire des) - L'espace - Espace et relativité sciences (histoire des) - La lumière - Échec du mécanisme et émergence du concept de champ sciences (histoire des) - La matière - Le calcul infinitésimal trajectoire vecteur vectoriel (espace) vitesse