Le calcul différentiel (Travaux Pratiques Encadrés - Espaces pédagogiques interactifs)

« sinus correspondant aux milieux considérés.

Comme Fermat l'avait remarqué, la détermination d'un minimum (ou d'un maximum) se ramène à un calcul de tangente .

Pour l'exprimer plus précisément, la tangente d'une courbe est « horizontale » en ses points extrêmes.

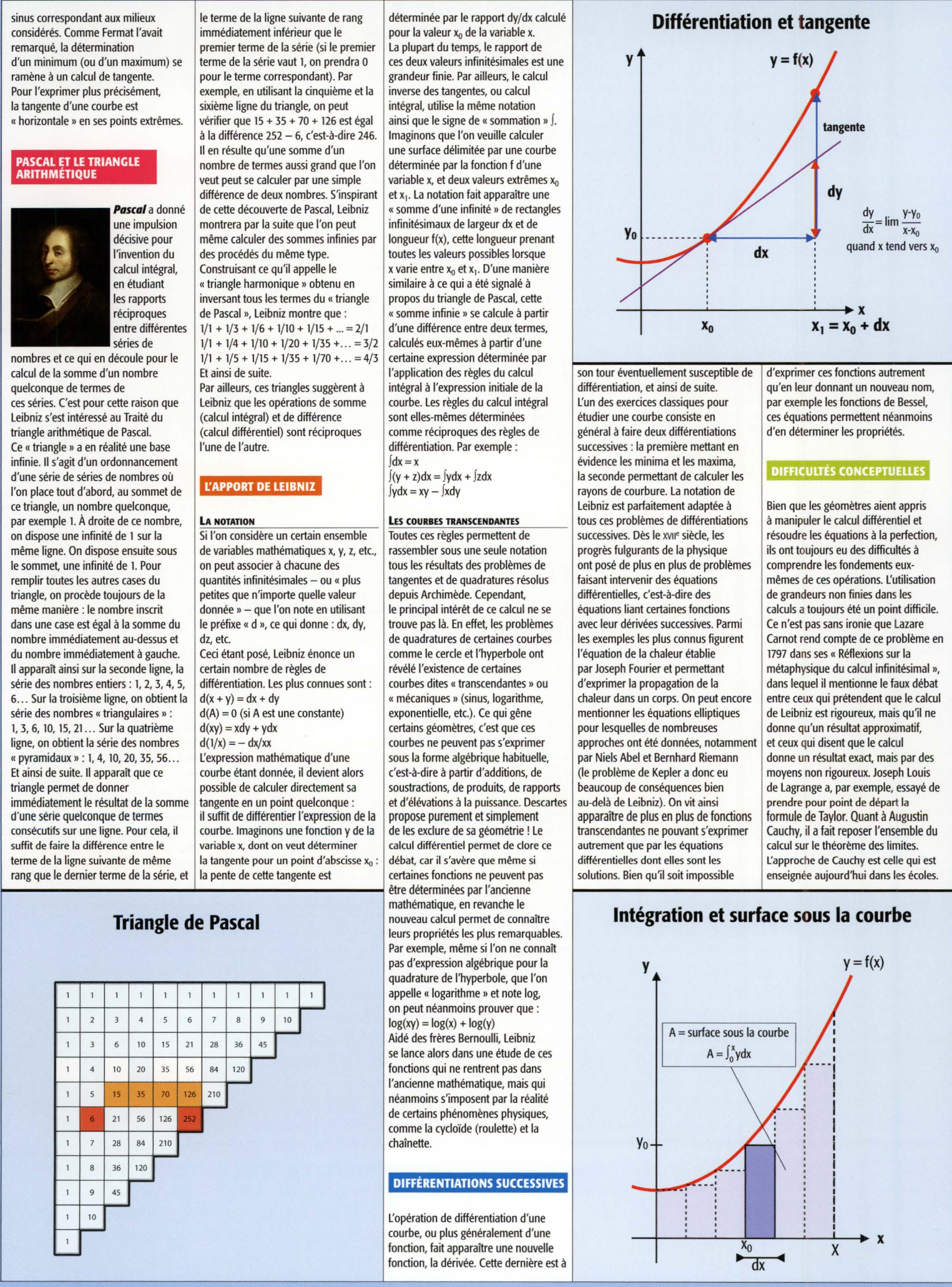
PASCAL ET LE TRIANGLE ARITHMÉTIQUE Pascal a donné une impulsion décisive pour l'invention du calcul intégral, en étudiant les rapports réciproques entre différentes séries de nombres et ce qui en découle pour le calcul de la somme d'un nombre quelconque de termes de ces séries.

C'est pour cette raison que Leibniz s 'est intéressé au Traité du triangle arithmétique de Pascal.

Ce «triangle " a en réalité une base infinie.

Il s'agit d'un ordonnancement d'une série de séries de nombres où l'on place tout d'abord, au sommet de ce triangle , un nombre quelconque, par exemple 1.

À droite de ce nombre, on dispose une infinité de 1 sur la même ligne.

On dispose ensuite sous le sommet, une infinité de 1.

Pour remp lir toutes les autres cases du triangle , on procède toujours de la même manière : le nombre inscrit dans une case est égal à la somme du nombre immédiatement au-dessus et du nombre immédiatement à gauche.

Il apparaît ainsi sur la seconde ligne, la série des nombres entiers : 1, 2, 3 , 4, 5, 6 ...

Sur la troisième ligne, on obtient la série des nombres " triangulaires " : 1, 3, 6, 10, 15, 21 ...

Sur la quatrième ligne , on obtient la série des nombres "pyramidaux" : 1, 4, 10, 20, 35, 56 ...

Et ainsi de suite.

Il apparaît que ce triangle permet de don ner immédiatement le résultat de la somme d 'une série quelconque de termes consécutifs sur une ligne.

Pour cela, il suffit de faire la différence entre le terme de la ligne suivante de même rang que le dernier terme de la série , et le terme de la ligne suivante de rang immédiatement inférieur que le premier terme de la série (si le premier terme de la série vaut 1, on prendra 0 pour le terme correspondant) .

Par exemple , en utilisant la cinquième et la sixième ligne du triangle, on peut vérifier que 15 + 35 + 70 + 126 est égal à la différence 252- 6, c'est-à-dire 246.

Il en résulte qu'une somme d'un nombre de termes aussi grand que l'on veut peut se calculer par une simple différence de deux nombres .

S'inspirant de cette découverte de Pascal, Leibniz montrera par la suite que l'on peut même calculer des sommes infinies par des procédés du même type .

Construisant ce qu'il appelle le « triangle harmonique » obtenu en inversant tous les termes du « triangle de Pascal », Leibniz montre que : 1/1 + 1/3 + 1/6 + 1/10 + 1 /15 + ...

= 2 /1 1/1 + 1/4 + 1/10 + 1/20 + 1/35 + ...

= 3/2 1 / 1 + 1/5 + 1/15 + 1/35 + 1/70 + ...

= 4/3 Et ainsi de suite .

Par ailleurs, ces triangles suggèrent à Leibniz que les opérations de somme (calcul intégral) et de différence (calcul différentiel) sont réciproques l'une de l'autre.

L'APPORT DE LEIBNIZ lA NOTATION Si l'on considère un certain ensemble de variables mathématiques x , y, z, etc., on peut associer à chacune des quantités infinitésimales -ou « plus petites que n'importe quelle valeur donnée » -que l'on note en utilisant le préfixe « d », ce qui donne : dx, dy, dz, etc.

Ceci étant posé , Leibniz énonce un certain nombre de règles de différentiation .

Les plus connues sont : d(x +y)= dx +dy d(A) = 0 (si A est une constante) d(xy) = xdy + ydx d(l/x) =- dxfxx !:expression mathématique d 'une courbe étant donnée, il devient alors possible de calculer directement sa tangente en un point quelconque : il suffit de différentier l'expression de la courbe.

Imaginons une fonction y de la variable x, dont on veut déterminer la tangente pour un point d'abscis se >. »