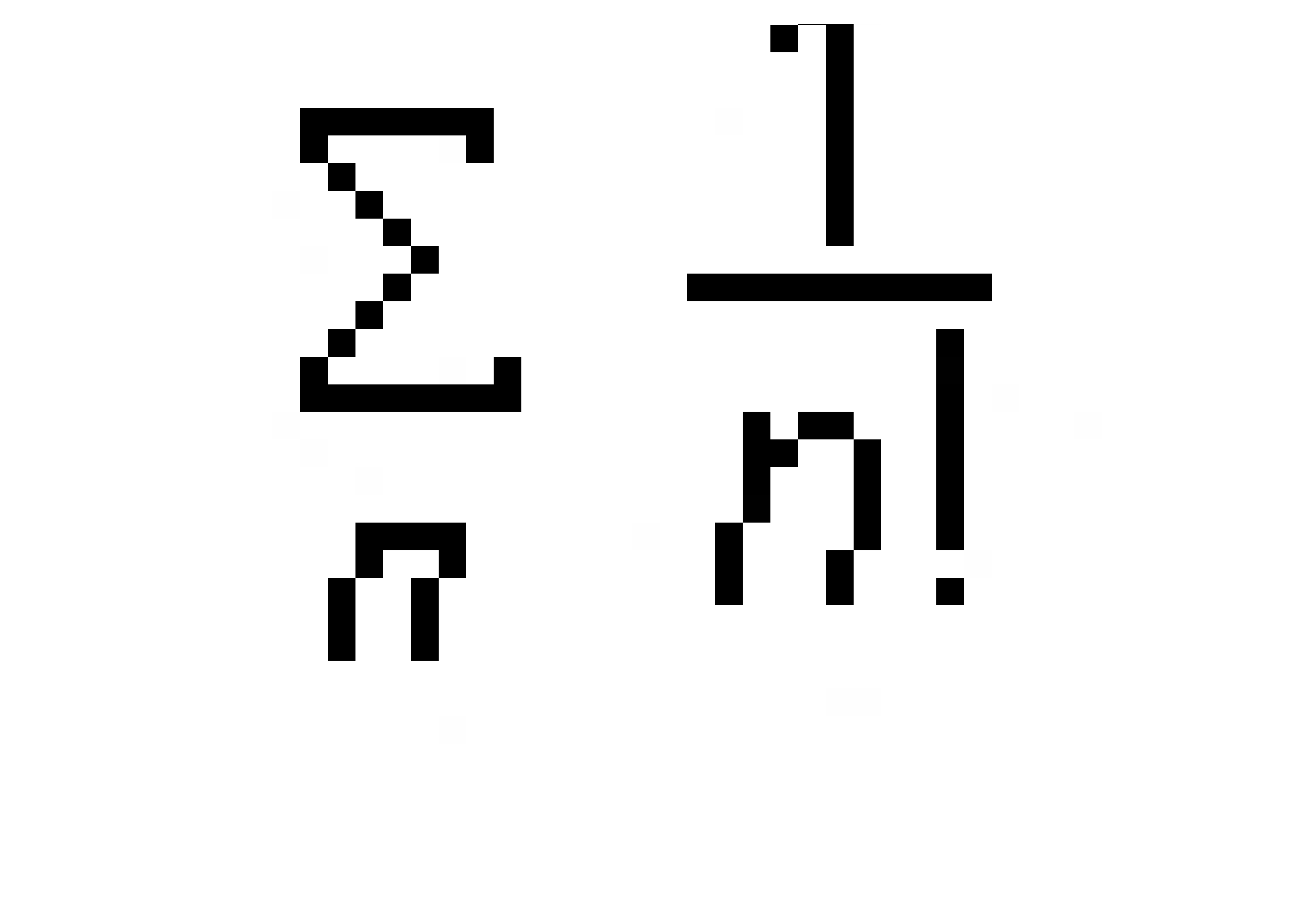e - mathématiques.

e - mathématiques. 1 PRÉSENTATION e (mathématiques), nombre réel, dit exponentiel et noté de sa première initiale e, intervenant dans différentes branches des mathématiques et dans toutes les disciplines scientifiques utilisant un formalisme mathématique. Depuis sa définition au XVIIe siècle, de nombreux mathématiciens cherchent à déterminer le plus grand nombre possible de ses décimales ; sa valeur approchée, à 10-24 près, est égale à : 2,718 281 828 459 045 235 360 287. 2 FONCTION EXPONENTIELLE Ce réel est notamment la base d'une fonction : la fonction exponentielle d'une variable x, notée exp (x) ou ex. Cette dernière est la fonction réciproque du logarithme népérien, noté ln et défini en 1614 par le mathématicien John Néper (1550-1617). La fonction exponentielle intervient dans la résolution de nombreux problèmes, en particulier dans les phénomènes physiques dépendant de deux variables x et y, caractérisées par un taux de variation ? y / ? x proportionnel à y. L'évolution de la variable y, ne dépendant que de celle de la variable x, est déterminée par la résolution de l'équation différentielle du premier ordre de type : y' = dy / dx = ky où k est un réel quelconque, et de solution générale : y = A.ekx où A est la valeur particulière de la variable y lorsque la variable x est nulle. 3 PROPRIÉTÉS ET APPLICATIONS DU RÉEL E Le nombre e intervient aussi dans la notation exponentielle des nombres complexes. Pour tout complexe z, tel que : z = x + iy où i est le nombre imaginaire pur tel que i2 = - 1, on a : ez = ex.eiy avec eiy = cos y + i.sin y En particulier, on a : ei p = - 1 (formule d'Euler) formule remarquable car elle met en relation e, i et p, qui sont, tous trois, des nombres très particuliers. D'autre part, le réel e est un nombre irrationnel. Mieux encore, le mathématicien français Charles Hermite (1822-1901) a établi en 1872 que le nombre e, est un réel transcendant, à l'image du réel pi ( p), dont la transcendance n'a été démontrée qu'une dizaine d'années après. Par définition un nombre est transcendant s'il n'est pas algébrique. Le nombre e n'est donc la racine d'aucun polynôme à coefficients entiers de quelque degré que ce soit, autrement dit il n'existe aucun ensemble d'entiers (an), où n est un entier naturel, qui satisfasse à la relation : Au XVIIIe siècle, les travaux du mathématicien Leonhard Euler, associés aux apports du calcul infinitésimal ont permis d'établir un développement en série des fonctions logarithme et exponentielle. Dès lors, e a été défini par la somme de la série : e = 1 + 1/2 ! + 1/3 ! +... = où n est un entier naturel ; e est aussi égal à la limite de l'expression (1 + 1/x)x, lorsque x tend vers l'infini. C'est encore l'unique réel tel que : Microsoft ® Encarta ® 2009. © 1993-2008 Microsoft Corporation. Tous droits réservés.