LES VOLUMES (Travaux Pratiques Encadrés - Espaces pédagogiques interactifs)

« appelons Vn le volume du prisme en escalier inscrit dans la pyramide où n désigne le nombre de« marches n.

Si on appelle B l'aire de la base de la pyramide et h sa hauteur, on a la valeur de l'aire de la base du k-ième prisme qui est égale à k2 B k =B2 n car les aires sont proportionnelles au carré des longueurs.

On a donc : h n-1 e Bh n-1 2 vn =- LB2=3 _L.k n k=l n n k=l Or les mathématiciens de l'époque connaissent bien cette formule qui permet de calculer la somme des carrés des n premiers nombres entiers : fy = n(n+l)(2n+l) k=l 6 On obtient donc : V " =~Bh(l-~ )(1- 21n ) On remarque que les quantités ljn et 1/2n deviennent de plus en plus petites au fur et à mesure que le nombre de «tranches n augmente.

Si bien qu'on pourrait les considérer comme négligeables.

L'erreur commise est un facteur (1 - 1 /n) (1 -1/2n).

Il vient alors la formule connue du volume d'une pyramide : V= 1/3 Bh C'est un embryon de ce que va être le calcul infinitésimal qu'Archimède met en place avec cette méthode.

Il ne manque plus que le passage à la limite , c'est-à-dire faire tendre le nombre de tranches vers l'infini et réduire l'épaisseur des tranches à une «quantité évanouissante n comme les appellera plus tard Leibniz (1646-1716), l'inventeur du calcul infinitésimal.

D'une manière plus moderne et en employant les limites, on a : V=!~V(n) v = lim ( .!.sh (I-..!_ )(1-_!__ )Î n~-l3 n 2n ) Comme lim (t-.!.. )=1 ·~- n et lim(l-_!__ J= 1 n-t- 2n on obtient: V=1 (38h DÉTERMINATION DU VOLUME DE LA SPHÈRE En 1629, Cavalieri, mathématicien Milanais, développe la méthode des indivisibles dans ses Exercitationes geometricoe , méthode qui allait inspirer ses successeurs pour le développement du calcul intégral.

Il fut l'élève de Galilée qui reconnut très vite son génie.

Inspiré par les travaux d'Euclide et d'Archimède, il calcule le volume de la sphère selon une méthode qui n'est pas sans rappeler celle de ce dernier.

Que dit ce principe? «Si deux solides ont méme hauteur et si des sections qui sont obtenues par des plans parallèles aux bases de ces deux solides et à distances égales de celles-ci sont dans un rapport donné, alors les volumes des deux solides sont aussi dans le méme rapport " Cavalieri considère que tout solide est la somme de morceaux de surfaces planes et donc que le volume de ce solide est la somme des aires de ces surfaces, c'est le principe des indivisibles.

Ce principe fut très contesté, notamment par Guldin qui montra à travers un exemple qu'il pouvait déboucher sur des résultats faux.

Il reste qu'il est historiquement fondateur du calcul infinitésimal.

Certes ce principe est peu rigoureux mais il est souvent efficace et permet de comparer les volumes de deux solides de formes apparemment très différentes.

Pour l'illustrer, prenons un jeu de carte, empilées les unes sur les autres.

Chaque carte représente un indivisible.

L'ensemb l e des cartes a un certain volume, si nous déformons le tas de cartes, par exemp le en en appuyant la paume de la main sur le jeu et en faisant tourne r les cartes, nous obtenons un autre solide, une espèce de vis dont le volume est le même que celui de notre tas de cartes parallélépipédique du départ.

Nous avons donc deux volumes qui ont la même hauteur (celle du jeu de carte) et qui sont coupés par des sections planes (chaque carte) qui sont dans un rapport de 1 puisque toutes les cartes ont la même aire.

On en conclut que les deux volumes sont égaux.

Pascal utilisera ce principe abondamment , notamment pour calculer le volume du solide engendré par une cycloïde tournant sur son axe.

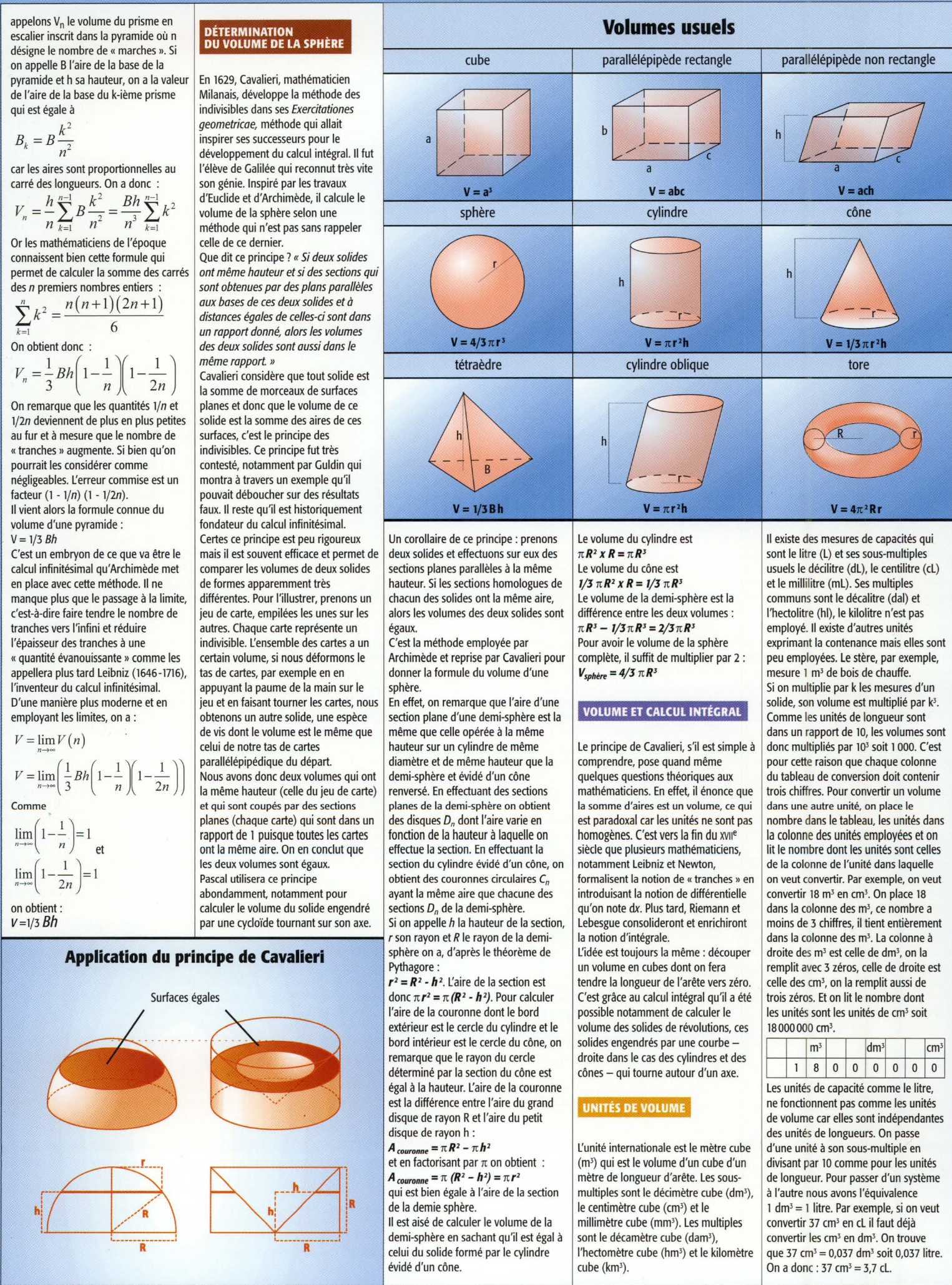
Volumes usuels cub e p a rallélépip ède rectang le ·G-D ,cg: / c V•a' V=abc sph ère c ylind re G hu Y •4/3nr• Y •nr•lll tétraèdre cyl indre oblique ~ r ~ W l W Un corollai r e de ce principe : prenons deux solides et effectuons sur eux des sections planes parallèles à la même hauteur .

Si les sections homo logues de chacun des solides ont la même aire, alors les volumes des deux solides sont égaux .

C'est la méthode employée par Archimède et reprise par Cava lieri pour donner la formule du volume d 'une sphère.

En effet, on remarque que l'aire d'une section plane d'une demi-sphère est la même que celle opérée à la même hauteur sur un cylindre de même diamètre et de même hauteur que la demi-sphère et évidé d'un cône renversé.

En effectuant des sections planes de la demi -sphère on obtient des disques D n dont l'aire varie en fonction de la hauteur à laquelle on effectue la section.

En effectuant la section du cylindre évidé d'un cOne, on obtient des couronnes circulaires C n ayant la même aire que chacune des sections Dn de la demi-sphère .

Si on appe lle h la hauteur de la section, Le volume du cylindre est rrR'xR= rrR ' Le volume du cône est 1/J rrR' x R = 1/J rrR' Le volume de la demi-sphère est la différence entre les deux volumes : rrR' - 1/ J rrR ' = 2/Jrr R ' Pour avoir le volume de la sphère complète, il suffit de multiplier par 2 : VspMre = 4/J rrR' VOLUME ET CALCUL INTÉGRAL 1------------""""------------ -1 r son rayon et R le rayon de la demi­ Le principe de Cavalieri, s'il est simple à comprendre, pose quand même quelques questions théoriques aux mathématiciens.

En effet , il énonce que la somme d'aires est un volume, ce qui est paradoxa l car les unités ne sont pas homogènes .

C'est vers la fin du XVII' siècle que plusieurs mathématiciens, notamment Leibniz et Newton, formalisent la notion de « tranches n en introduisant la notion de différentielle qu'on note dx.

Plus tard, Riemann et Lebesgue consolideront et enrichiront la notion d'intégrale.

Application du principe de Cavalieri Surfaces égales R ._ ______ i _______ : sphère on a, d'après le théorème de Pythagore: r' = R'-h2 • L'aire de la section est donc rrr' = rr (R'-h').

Pour calculer l'aire de la couronne dont le bord extérieur est le cercle du cylindre et le bord intérieur est le cercle du cône, on remarque que le rayon du cercle déterminé par la section du cône est égal à la hauteur.

L'aire de la couronne est la différence entre l'aire du grand disque de rayon Ret l'aire du petit disque de rayon h : A couronnr = 1tR2 -nhl et en factorisant par rr on obtient : A couronne = rr (R ' - h') = rr r' qui est bien égale à l 'aire de la section de la demie sphère .

Il est aisé de calculer le volume de la demi-sphère en sachant qu'il est égal à celui du solide formé par le cylindre évidé d'un cône.

L'idée est toujours la même : découper un volume en cubes dont on fera tendre la longueur de l'arête vers zéro.

C'est grâce au calcul intégral qu'il a été possible notamment de calcu ler le volume des solides de révolutions, ces solides engendrés par une courbe - droite dans le cas des cylindres et des cônes- qui tourne autour d'un axe.

iii@iJ.!jiJ,!i@i L'unité internationale est le mètre cube (m') qui est le volume d'un cube d'un mètre de longueur d 'arête.

Les sous­ multiples sont le décimètre cube (dm '), le centimètre cube (cm') et le millimètre cube (mm ').

Les multiples sont le décamètre cube (dam '), l'hectomètre cube (hm ' ) et le kilomètre cube (km').

par a llé lépip è de non rectangle cône tor e Il existe des mesures de capacités qui sont le litre (L) et ses sous-multiples usuels le décilitre (dl), le centilitre (cl) et le millilitre (ml).

Ses multiples communs sont le décalitre (dai) et l'hectolitr e (hl), le kilolitre n'est pas employé .

Il existe d'autres unités exprimant la contenance mais elles sont peu emp loyées.

Le stère, par exemple, mesure 1 m ' de bois de chauffe.

Si on multiplie par k les mesures d'un solide, son volume est multiplié par k'.

Comme les unités de longueur sont dans un rapport de 10, les volumes sont donc multipliés par 10' soit 1 000.

C'est pour cette raison que chaque colonne du tableau de conversion doit contenir trois chiffres.

Pour convertir un volume dans une autre unité, on place le nombre dans le tableau, les unités dans la colonne des unités employées et on lit le nombre dont les unités sont celles de la colonne de l'unité dans laquelle on veut convertir.

Par exemple , on veut convertir 18 m'en cm'.

On place 18 dans la colonne des m ', ce nombre a moins de 3 chiffres, il tient entièrement dans la colonne des m '.

La colonne à droite des m ' est celle de dm', on la remplit avec 3 zéros, celle de droite est celle des cm', on la remplit aussi de trois zéros.

Et on lit le nombre dont les unités sont les unités de cm' soit 18000000 cm' .

Les unités de capacité comme le litre, ne fonctionnent pas comme les unités de volume car elles sont indépendantes des unité s de longueurs.

On passe d'une unité à son sous-multip le en divisant par 10 comme pour les unités de longueur.

Pour passer d'un système à l'autre nous avons l'équivalence 1 dm' = 1 litre.

Par exemple, si on veut convertir 37 cm' en cl il faut déjà convertir les cm' en dm'.

On trouve que 37 cm' = 0,037 dm' soit 0,037 litre.

On a donc : 37 cm'= 3,7 cl.. »