Le calcul différentiel (histoire et principe)
Publié le 23/10/2012

Extrait du document

UN LANGAGE REVOLUTIONNAIRE
Fondé sur l'utilisation de grandeurs infinitésimales, le calcul différentiel peut paraître éloigné de la réalité de tout un chacun. Cependant, il a été crucial dans la résolution de nombreux problèmes mathématiques, auparavant insolubles, liés à des approches pratiques telles que le calcul de vitesses et d'accélérations.
Utile dans un ensemble de domaines (optique, mathématiques, astronomie...), le calcul différentiel intervient chaque fois qu’un certain nombre de grandeurs physiques varient les unes par rapport aux autres, c'est-à-dire tout le temps. Sans lui, il est certain que la révolution scientifique et industrielle n'aurait pas eu lieu.
Dans l'Antiquité, deux types généraux de problèmes géométriques se sont posés, pour lesquels il ne semblait exister que des solutions particulières : le calcul des tangentes et le calcul des quadratures (à la base, calcul de surfaces et volumes). Bien longtemps après, l'astronome Johannes Kepler se trouve
confronté à un problème similaire qui paraît insoluble. En effet, après avoir découvert que la trajectoire des planètes est elliptique, il tente de calculer la surface d'un secteur elliptique mais n'arrive qu'à une approximation. Il lance, dans son ouvrage « Astronomie nouvelle », un appel aux géomètres pour trouver un nouvel outil mathématique afin de résoudre ce problème.
Des savants comme Pierre de Fermât, Blaise Pascal, Isaac Newton, Gottfried Leibniz et bien d'autres se lancent dans cette recherche. C'est finalement Leibniz qui découvre le calcul différentiel et intégral. Cependant il existe une polémique à ce sujet, certains pensant que Newton aurait inventé un calcul équivalent à celui de Leibniz, appelé calcul des fluxions. Certes, Leibniz a le premier publié ses résultats en 1684, mais Newton l'avait accusé de plagiat. Toutefois, cette accusation n’est pas très vraisemblable, car le calcul des fluxions évacue l'aspect essentiel du calcul différentiel - en l'occurrence l’utilisation de grandeurs infinitésimales, les différentielles - pour n'y laisser
subsister que des grandeurs finies, ce qui lui impose de prendre l'une des variables comme référence fixe.
DEUX PROBLEMES RÉCIPROQUES
Le calcul des tangentes et le calcul des quadratures font surgir certains paradoxes qui seront à la base de la découverte du calcul différentiel. En leur apportant une solution générale, Leibniz va montrer que chacun de ces deux problèmes était le réciproque de l'autre.
Le calcul des tangentes
Considérons une sécante, c'est-à-dire une droite définie par deux points sur une courbe. Imaginons que l'un des points est fixe et que l'autre se déplace le long de la courbe ; on engendre ainsi toute une famille de sécantes. Il existe une singularité dans cette famille : la droite obtenue quand les deux points se confondent. Cette droite tangente, définie pour les points suffisamment réguliers sur une courbe est une caractéristique intrinsèque de la courbe ; elle ne dépend pas de la façon dont on fait tendre les points l'un vers l'autre.
Elle a du reste une interprétation bien concrète puisqu'il s'agit de la droite portant la direction de la vitesse instantanée d'un mobile qui se déplacerait le long de cette courbe. Toutefois, malgré des implications mécaniques et sa réalité géométrique, la détermination de la tangente à une courbe requiert des notions dépassant le cadre de la géométrie classique. On obtient cette tangente par un « passage à la limite », c'est-à-dire en faisant tendre vers zéro la distance entre deux points de la courbe ; la tangente est la limite des sécantes joignant ces points. C'est le calcul différentiel qui fournit les outils mathématiques nécessaires à cette opération.

«
sinus correspondant aux milieux considérés.
Comme Fermat l'avait remarqué, la détermination d'un minimum (ou d'un maximum) se ramène à un calcul de tangente .
Pour l'exprimer plus précisément, la tangente d'une courbe est « horizontale » en ses points extrêmes.
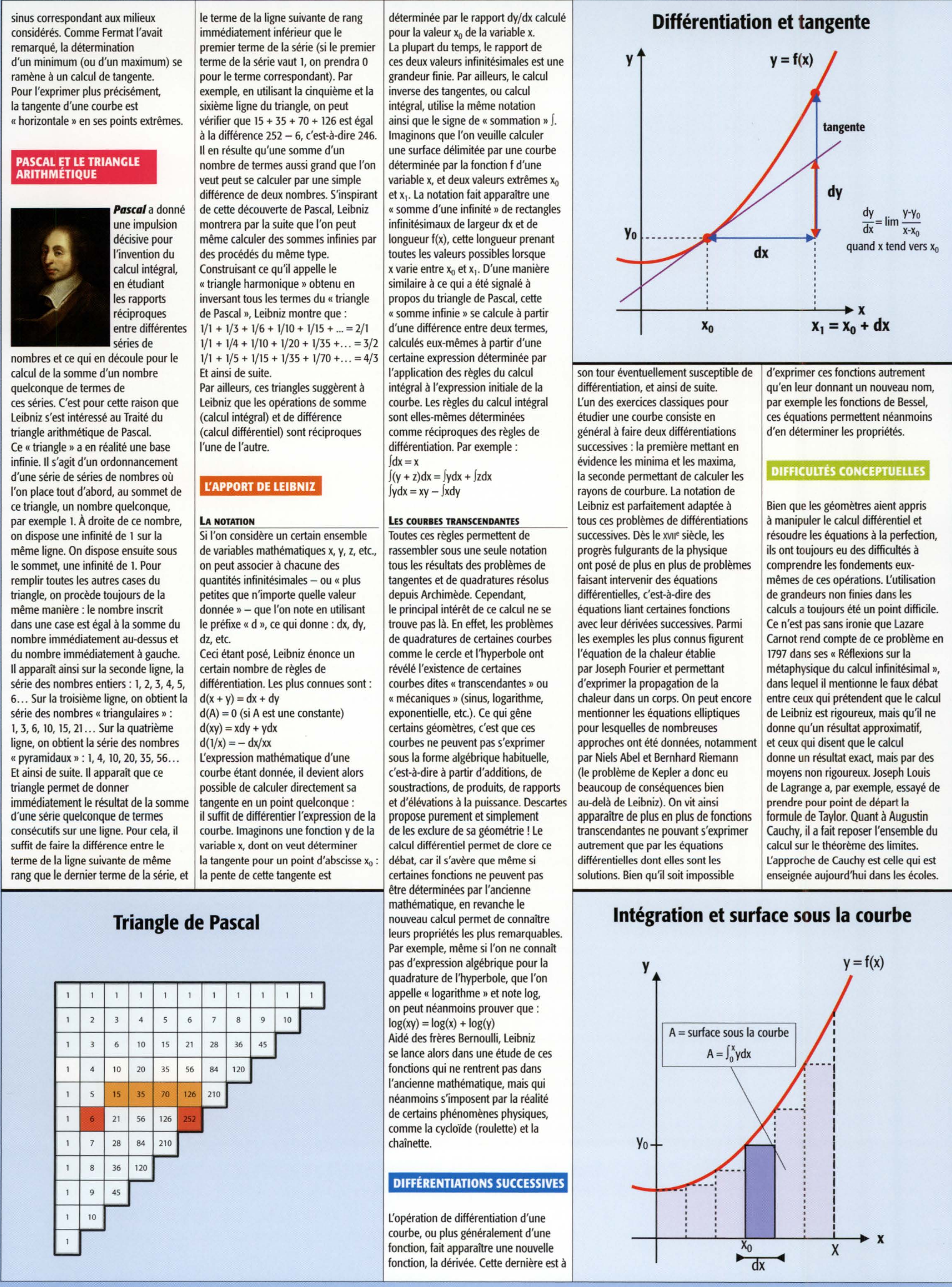
PASCAL ET LE TRIANGLE ARITHMÉTIQUE
Pascal a donné une impulsion décisive pour l'invention du calcul intégral, en étudiant les rapports réciproques entre différentes séries de nombres et ce qui en découle pour le calcul de la somme d'un nombre quelconque de termes de ces séries.
C'est pour cette raison que Leibniz s 'est intéressé au Traité du triangle arithmétique de Pascal.
Ce «triangle " a en réalité une base infinie.
Il s'agit d'un ordonnancement d'une série de séries de nombres où l'on place tout d'abord, au sommet de ce triangle , un nombre quelconque, par exemple 1.
À droite de ce nombre, on dispose une infinité de 1 sur la même ligne.
On dispose ensuite sous le sommet, une infinité de 1.
Pour remp lir toutes les autres cases du triangle , on procède toujours de la même manière : le nombre inscrit dans une case est égal à la somme du nombre immédiatement au-dessus et du nombre immédiatement à gauche.
Il apparaît ainsi sur la seconde ligne, la série des nombres entiers : 1, 2, 3 , 4, 5, 6 ...
Sur la troisième ligne, on obtient la série des nombres " triangulaires " : 1, 3, 6, 10, 15, 21 ...
Sur la quatrième ligne , on obtient la série des nombres "pyramidaux" : 1, 4, 10, 20, 35, 56 ...
Et ainsi de suite.
Il apparaît que ce triangle permet de don ner immédiatement le résultat de la somme d 'une série quelconque de termes consécutifs sur une ligne.
Pour cela, il suffit de faire la différence entre le terme de la ligne suivante de même rang que le dernier terme de la série , et
le terme de la ligne suivante de rang immédiatement inférieur que le premier terme de la série (si le premier terme de la série vaut 1, on prendra 0 pour le terme correspondant) .
Par exemple , en utilisant la cinquième et la sixième ligne du triangle, on peut vérifier que 15 + 35 + 70 + 126 est égal à la différence 252- 6, c'est-à-dire 246.
Il en résulte qu'une somme d'un nombre de termes aussi grand que l'on veut peut se calculer par une simple différence de deux nombres .
S'inspirant de cette découverte de Pascal, Leibniz montrera par la suite que l'on peut même calculer des sommes infinies par des procédés du même type .
Construisant ce qu'il appelle le « triangle harmonique » obtenu en inversant tous les termes du « triangle de Pascal », Leibniz montre que : 1/1 + 1/3 + 1/6 + 1/10 + 1 /15 + ...
= 2 /1 1/1 + 1/4 + 1/10 + 1/20 + 1/35 + ...
= 3/2
1 / 1 + 1/5 + 1/15 + 1/35 + 1/70 + ...
= 4/3 Et ainsi de suite .
Par ailleurs, ces triangles suggèrent à Leibniz que les opérations de somme (calcul intégral) et de différence (calcul différentiel) sont réciproques l'une de l'autre.
L'APPORT DE LEIBNIZ
lA NOTATION Si l'on considère un certain ensemble de variables mathématiques x , y, z, etc., on peut associer à chacune des quantités infinitésimales -ou « plus petites que n'importe quelle valeur donnée » -que l'on note en utilisant le préfixe « d », ce qui donne : dx, dy, dz, etc.
Ceci étant posé , Leibniz énonce un certain nombre de règles de différentiation .
Les plus connues sont : d(x +y)= dx +dy d(A) = 0 (si A est une constante) d(xy) = xdy + ydx d(l/x) =- dxfxx !:expression mathématique d 'une courbe étant donnée, il devient alors possible de calculer directement sa tangente en un point quelconque : il suffit de différentier l'expression de la courbe.
Imaginons une fonction y de la variable x, dont on veut déterminer la tangente pour un point d'abscis se >.
»
↓↓↓ APERÇU DU DOCUMENT ↓↓↓
Liens utiles
- Histoire du calcul différentiel (TPE)
- Le calcul différentiel (Travaux Pratiques Encadrés - Espaces pédagogiques interactifs)
- LE VIVANT REQUIERT-IL UN PRINCIPE SPÉCIFIQUE D'EXPLICATION ? QUELQUES ÉLÉMENTS DE RÉFLEXION SUR L'HISTOIRE DE LA PENSÉE BIOLOGIQUE.
- différentiel (calcul).
- FERMAT, Pierre de (1601-1665) Mathématicien, il est un précurseur dans divers domaines : calcul différentiel, géométrie analytique et calcul des probabilités.