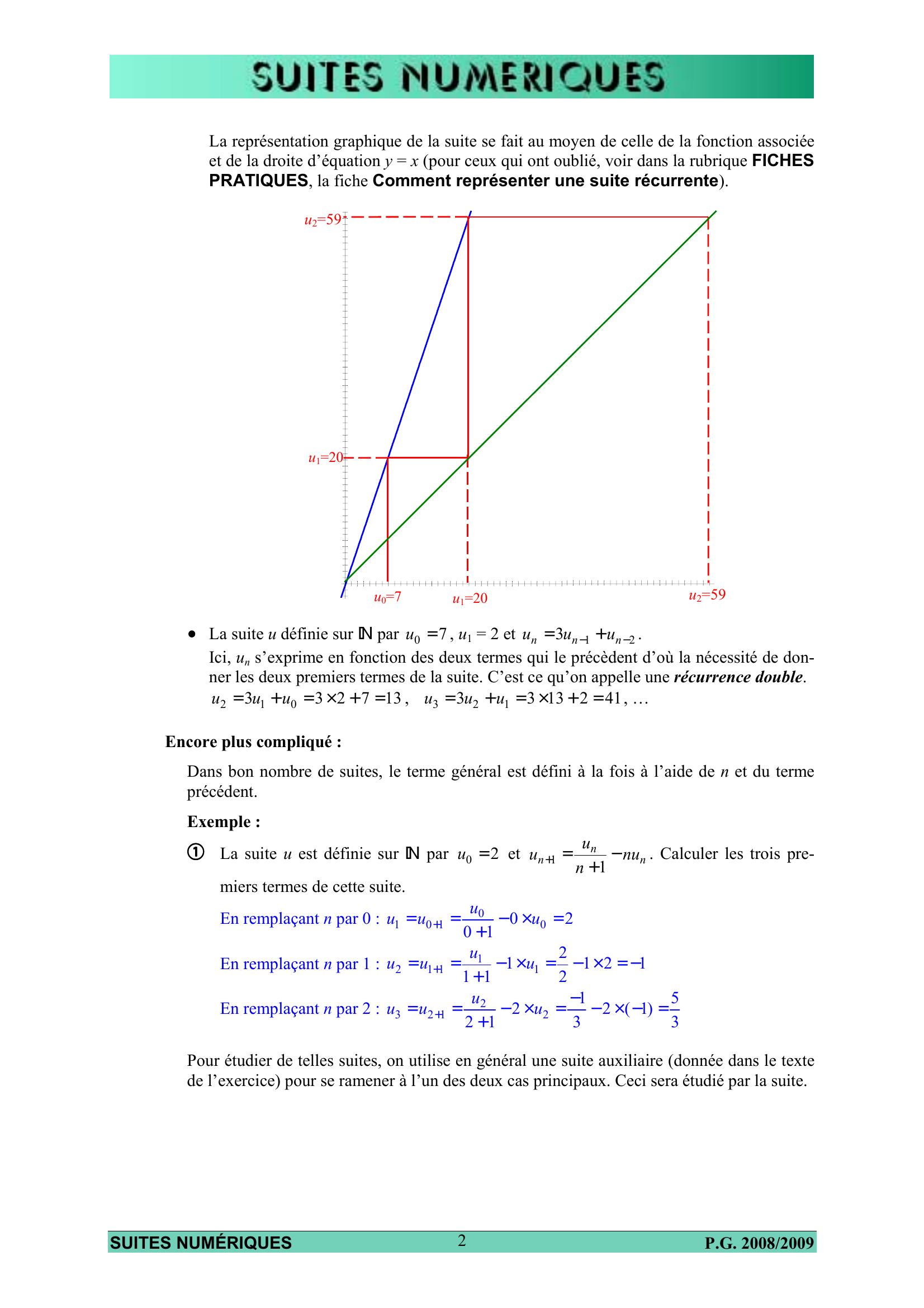
§1. Pour bien débuter 1. Rappels de première On distingue traditionnellement deux types principaux de suites : Suite définie par son terme général : Le terme général un de la suite est donné directement en fonction de n, ce qui permet de calculer directement n’importe quel terme de la suite et, en général, d’utiliser les propriétés de la fonction associée à la suite. n a pour fonction associée la fonction Exemple : La suite u définie sur N par un = 2n + 1 x 8 8 . u8 = f (8) = f :x! = . Les variations de la fonction donnent directe2x + 1 2 × 8 + 1 17 ment celles de la suite et la limite en +∞ de la fonction donne la limite de la suite. La représentation graphique de la suite se fait sur celle de la fonction puisque les entiers sont des réels parmi tant d’autres. Suite définie par récurrence : Chaque terme s’exprime en fonction de celui qui le précède ou de certains termes qui le précèdent. Exemples : • La suite u définie sur N par u0 = 7 et un +1 = 3un − 1 a pour fonction associée la fonction f : x ! 3 x − 1 . Pour calculer u3, il faut d’abord calculer u1 et u2 : u1 = f ( u0 ) = 3u0 − 1 = 3 × 7 − 1 = 20 , u2 = f ( u1 ) = 3u1 − 1 = 3 × 20 − 1 = 59 et enfin u3 = f ( u2 ) = 3u2 − 1 = 3 × 59 − 1 = 176 Inutile de dire que si l’on veut calculer u153 sans calculatrice … A propos de calculatrice, sachez qu’il suffit de taper le premier terme de la suite et d’appuyer sur la touche ENTER (Texas) ou EXE (Casio) puis de taper le texte de la suite en remplaçant un par la touche Ans puis d’appuyer sur ENTER ou EXE autant de fois que vous voulez pour obtenir les termes suivants : SUITES NUMÉRIQUES 1 P.G. 2008/2009 La représentation graphique de la suite se fait au moyen de celle de la fonction associée et de la droite d’équation y = x (pour ceux qui ont oublié, voir dans la rubrique FICHES PRATIQUES, la fiche Comment représenter une suite récurrente). u2=59 u1=20 u0=7 u2=59 u1=20 • La suite u définie sur N par u0 = 7 , u1 = 2 et un = 3un −1 + un − 2 . Ici, un s’exprime en fonction des deux termes qui le précèdent d’où la nécessité de donner les deux premiers termes de la suite. C’est ce qu’on appelle une récurrence double. u2 = 3u1 + u0 = 3 × 2 + 7 = 13 , u3 = 3u2 + u1 = 3 × 13 + 2 = 41 , … Encore plus compliqué : Dans bon nombre de suites, le terme général est défini à la fois à l’aide de n et du terme précédent. Exemple : B La suite u est définie sur N par u0 = 2 et un +1 = miers termes de cette suite. un − nun . Calculer les trois pren +1 u0 − 0 × u0 = 2 0 +1 u 2 En remplaçant n par 1 : u2 = u1+1 = 1 − 1 × u1 = − 1 × 2 = −1 1+1 2 u2 −1 5 − 2 × u2 = − 2 × (−1) = En remplaçant n par 2 : u3 = u2+1 = 2 +1 3 3 En remplaçant n par 0 : u1 = u0+1 = Pour étudier de telles suites, on utilise en général une suite auxiliaire (donnée dans le texte de l’exercice) pour se ramener à l’un des deux cas principaux. Ceci sera étudié par la suite. SUITES NUMÉRIQUES 2 P.G. 2008/2009 2. La factorielle d’un entier naturel Définition : La factorielle d’un entier naturel n non nul est le produit de tous les entiers de 1 à n. On la note : n! = 1×2×…×n. Exemples : 5! = 1×2×3×4×5 = 120. 8! = 1×2×3×4×5×6×7×8 = 40320. Votre calculatrice peut donner les factorielles. Consultez la fiche Comment afficher une factorielle dans la rubrique FICHES PRATIQUES. Vous aurez souvent à établir des propriétés faisant intervenir des factorielles. Exemples : C Exprimer (n + 1)! en fonction de n! Il suffit d’appliquer la définition (en détaillant un peu les points de suspension, c'est-àdire en écrivant quelques facteurs intermédiaires) : (n + 1)! = 1 × 2 × … × (n − 1) × n × (n + 1) (n + 1)! = D × (n + 1) n! Montrer que 8! − 6! = 55×6! 8!− 6! = 1 × 2 × … × 6 × 7 × 8 − 6! 8!− 6! = 6! × 7 × 8 − 6! 8!− 6! = 6!× 56 − 6! 8!− 6! = 6!× ( 56 − 1) 8!− 6! = 6!× 55 E Montrer que, pour tout entier naturel non nul, on a ( n + 2)!− 2n ! = n !n( n + 3) . (n + 2)!− 2n ! = 1 × 2 × … × n × (n + 1) × (n + 2) − 2n ! (n + 2)!− 2n ! = × (n + 1) × (n + 2) − 2n ! n! (n + 2)!− 2n ! = n !× [ (n + 1) × (n + 2) − 2] ( (n + 2)!− 2n ! = n !× ( n (n + 2)!− 2n! = n !× n 2 + 3n + 2 − 2 2 + 3n (n + 2)!− 2n ! = n !× n ( n + 3) ) ) Extension de la définition : Pour que l’égalité (n + 1)! = n!× ( n + 1) reste valable pour n = 0 (et pour d’autres raisons que vous verrez par la suite), on est amené à poser : 0! = 1. Effectivement, remplacez n par 0 dans l’égalité. On obtient : 1! = 0!× 1 . SUITES NUMÉRIQUES 3 P.G. 2008/2009 3. Le symbole Σ Il est utilisé pour simplifier l’écriture d’une somme, à condition que tous les termes de cette somme aient une « forme » commune. Exemples : • 32 + 42 + 52 + 62 + 7 2 se note i =7 ∑i2 7 ∑i2 . ou souvent i =3 i =3 A noter que la lettre choisie est une lettre « muette », c'est-à-dire que vous pouvez la remplacer par celle que vous voulez. • 1 + 2 + 3 + 2 + 5 + 6 se note 6 ∑ k. k =1 • Un peu plus compliqué : 1 + 3 + 5 + 7 + 9 + 11 , qui est la somme de nombres impairs consécutifs se note : 5 ∑ (2i + 1) puisque 2i+1 est la forme générale des nombres impairs. Il i =0 ne reste plus qu’à trouver les valeurs extrêmes de i en résolvant : 2i + 1 = 1 ⇔ 2i = 0 ⇔ i = 0 et 2i + 1 = 11 ⇔ 2i = 10 ⇔ i = 5 . A noter qu’une somme a une infinité d’écritures à l’aide du symbole Σ. A titre d’exemple, un nombre impair pouvant aussi bien s’écrire sous la forme 2i – 1, ou 2i + 3, ou …, la dernière somme donnée peut également s’écrire : 6 ∑ (2i − 1) ou i =1 4 ∑ (2i + 3) ou … i =−1 Pour être très correct, personne ne sait ce que recouvrent des points de suspension. C’est pourquoi le symbole Σ sera, tôt ou tard, la seule solution correcte d’écriture. Exemples : F Ecrire, à l’aide du symbole Σ, les sommes : 1 2 3 2008 + + +…+ a. 2 3 4 2009 1 2 3 2008 2008 i + + +…+ =∑ 2 3 4 2009 i =1 i + 1 1 2 3 4 17 b. + + + +…+ 4 9 16 25 324 1 2 3 4 17 1 2 3 4 17 17 i + + + +…+ = 2 + 2 + 2 + 2 +…+ 2 = ∑ 2 4 9 16 25 324 2 3 4 5 18 i =1 (i + 1) G La suite u est définie sur N par : un = ∑ k2 . Calculer u3. k =1 k + 1 n k2 12 22 32 1 4 9 49 = + + = + + = 2 3 4 12 k =1 k + 1 1 + 1 2 + 1 3 + 1 3 u3 = ∑ H Simplifier : 1 n −1 1 ∑ i − ∑ k +1 . i =1 k =2 n 1 n −1 1 1? ?1 1 1? 1 3 ?1 1 1 1 ∑ i − ∑ k +1 = ?1 + 2 + 3 + 4 +…+ n ? − ? 3 + 4 +…+ n ? =1+ 2 = 2 . ? ? ? ? i =1 k =2 n SUITES NUMÉRIQUES 4 P.G. 2008/2009 §2. Variations 1. Suites définies par leur terme général 1ère méthode : Comparer directement u n + 1 à u n. Pour cela on utilise en général les règles usuelles sur les inégalités et les variations des fonctions élémentaires. Exemple : 1& Etudier le sens de variation de la suite u définie sur N par un = n 2 + 2 . On commence par calculer u n +1 : un +1 = (n + 1) 2 + 2 . Point-méthode : pour comparer deux nombres d’écritures voisines, on part des éléments qui diffèrent puis on greffe peu à peu les éléments communs. n < n +1 donc n2 < (n +1)2 car la fonction x ! x 2 est strictement croissante sur [0 ; +∞[ n2 + 2 < (n +1)2 + 2 car x ! x + 2 est strictement croissante sur R n 2 + 2 < ( n + 1)2 + 2 car x ! x est strictement croissante sur [0 ; +∞[ u n < u n +1 La suite (u n) est strictement croissante. 2ème méthode : Etudier le signe de la différence u n + 1 − u n. Exemple : 1* n +1 . n+3 n + 1 + 1 n + 1 n + 2 n + 1 (n + 2)(n + 3) − (n + 1)(n + 4) ∀n ∈ N un +1 − un = − = − = (n + 4)(n + 3) n +1+ 3 n + 3 n + 4 n + 3 Etudier le sens de variation de la suite u définie sur N par un = Point-méthode : pour une étude de signe, si ce signe n’est pas évident, on réduit au même dénominateur et on laisse le dénominateur factorisé. n 2 + 3n + 2n + 6 − n 2 − 4n − n − 4 2 = (n + 4)(n + 3) (n + 4)(n + 3) ∀n ∈N un +1 − un > 0 un +1 > un La suite u est strictement croissante. u 3ème méthode : Si tous les termes de la suite sont de même signe, on peut comparer n+1 à 1. un Exemple : 1( 1. Montrer que, pour tout entier naturel n non nul, (n +1)! = (n +1)×n! (n +1)! = 1×2×…×n×(n +1) = n!×(n +1) n! 2. Etudier le sens de variation de la suite (u n) définie, pour n∈N*, par un = . n +1 (n + 1)! un +1 (n + 1)!(n + 1) (n + 1) × n!× (n + 1) (n + 1) × (n + 1) ∀n ∈N* = n+2 = = = n! un ( n + 2)n! (n + 2) × n! n+2 n +1 u n 2 + 2n + 1 1 un +1 u ∀n ∈N* n +1 = =n+ > n or n ≥ 1 donc n +1 > 1 . un n+2 n+2 un un Puisque tous les termes sont strictement positifs, on multiplie par u n sans changer le sens : u n +1 > u n. La suite u est strictement croissante. ∀n ∈N un +1 − un = SUITES NUMÉRIQUES 5 P.G. 2008/2009 4ème méthode : Utiliser les variations de la fonction associée à la suite. Exemples : 2) Etudier le sens de variation de la suite (u n) définie, pour n∈N, par un = 2n + 8 . n+3 2x + 8 . Cette fonction est une foncx+3 tion rationnelle. Elle est donc dérivable sur son ensemble de définition. 2 × ( x + 3) − (2 x + 8) ×1 −2 ∀x ∈R−{−3} f '( x) = = 2 ( x + 3) ( x + 3)2 Sa dérivée étant strictement négative sur [0 ; +∞[, f est strictement décroissante sur [0 ; +∞[. La suite u est donc strictement décroissante. La fonction associée à la suite est la fonction f : x ! 2! Etudier le sens de variation de la suite (u n) définie, pour n∈N, par un = 2n 2 − 7 n + 1 . Les variations de la fonction f : x ! 2 x 2 − 7 x + 1 (fonction du second degré - revoir le cours de première) sont résumées dans le tableau : Puisque 0 et 1 appartiennent à ]−∞ ; 7/4], la x −∞ suite est strictement décroissante du rang 0 au f (x) rang 1. Puisque 2 et tous ses suivants appartiennent à [7/4 ; +∞[, la suite est strictement croissante à partir du rang 2. En revanche, 1 et 2 n’étant pas dans le même intervalle, il est impossible d’utiliser les variations pour comparer u1 et u2. Dans ce cas, on calcule directement ces termes pour les comparer : u1 = −4 et u2 = −5. u1 > u2. La suite est strictement décroissante du rang 1 au rang 2. Au total, u est strictement décroissante du rang 0 au rang 2 et strictement croissante à partir du rang 2. Formule : − b 2a 7/4 +∞ 7 4 Pour terminer, un exemple plus … déroutant. 2@ Etudier le sens de variation de la suite u définie sur N* par k =2n 1 1 1 1 un = = + +…+ 2n n n +1 k =n k ∑ Point-méthode : dans ce type d’exercice, ajouter quelques termes intermédiaires dans chaque somme pour voir les termes qu’il y a en plus ou en moins. ∀n ∈N* un +1 − un = 1 1 1 1 1 1 1 1 ? ?1 + +…+ + + −? + + +…+ ? n +1 n + 2 2n 2n + 1 2(n + 1) ? n n + 1 n + 2 2n ? 1 1 1 2(n + 1)n + (2n + 1)n − 2(n + 1)(2n + 1) + − = 2n + 1 2( n + 1) n 2(n + 1)n(2n + 1) −3n − 2 u n +1 − u n < 0 u n +1 < u n ∀n ∈N* un +1 − un = 2(n + 1)n(2n + 1) La suite u est strictement décroissante. ∀n ∈N* un +1 − un = SUITES NUMÉRIQUES 6 P.G. 2008/2009 2. Suites définies par récurrence 1ère méthode : Comparer directement u n + 1 à u n. Exemple : 3! 2 Etudier le sens de variation de la suite u définie sur N par u 0 = −5 et un +1 = un + 4 . Rappelons tout d’abord la représentation d’une suite définie par récurrence au moyen de la fonction associée : 4 > 0 donc 2 2 un + 4 > un . La fonction x ! x étant strictement croissante sur [0 ; +∞[, 2 un + 4 > un c'est-à-dire un ≥ un , à plus 2 2 un + 4 > un et comme forte raison 2 un + 4 > un , un +1 > un . La suite u est strictement croissante. 2ème méthode : Etudier le signe de la différence u n + 1 − u n. Exemple : 3@ On considère la suite u définie u 0 = 5 et, pour tout entier naturel n, par 1? 4 ? un +1 = ? un + ? . 2? un ? a. Montrer, par récurrence, que tous les termes de la suite sont strictement supérieurs à 2. Un raisonnement par récurrence se fait en trois étapes : Initialisation : La propriété u n > 2 est vraie pour n = 0 puisque 5 > 2, u 0 > 2. Hérédité : Soit n un entier naturel quelconque. ? 1 u 2 + 4 − 4un 1 (un − 2) 2 1? 4 ? 1? 4 un +1 − 2 = ? un + ? − 2 = ? un + − 4 ? = × n = × 2? un ? 2? un un 2 un ? 2 Si u n > 2, alors u n − 2 > 0, (u n − 2)2 > 0, u n +1 − 2 > 0, u n +1 > 2. Conclusion : La propriété u n > 2 est vraie pour n = 0 et héréditaire à partir de n = 0. Le principe de récurrence permet d’affirmer qu’elle est vraie pour tout entier n à partir de 0. ∀n∈N u n > 2. b. Etudier le sens de variation de la suite. Pour tout entier naturel n, 2 ? 1? 4 ? 1 4 − un 1? 4 ? 1? 4 un +1 − un = ? un + ? − un = ? un + − 2un ? = ? − un ? = × 2? un ? 2? un un ? 2 ? un ? 2 1 (2 + un )(2 − un ) et comme 2 − u n < 0 d’après ce qui précède, un +1 − un = × 2 un u n +1 − u n < 0, u n +1 < u n, la suite est strictement décroissante. SUITES NUMÉRIQUES 7 P.G. 2008/2009 3ème méthode : Si tous les termes de la suite sont du même signe, comparer un+1 à 1. un Exemple : 3# Etudier le sens de variation de la suite u définie par u 0 = 7 et, pour n∈N, par u2 un +1 = n , après avoir montré que tous ses termes sont strictement positifs. un + 1 Un raisonnement par récurrenc...